二等辺三角形の公式(面積・高さ・角度・斜辺と周囲の長さ)
二等辺三角形
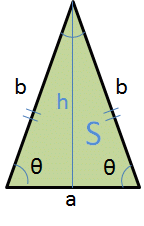
計算
斜辺の長さ
\[ b = \sqrt{h^2 + \frac{a^2}{4} } \]角度
\[ \theta = \tan^{-1}( \frac{2h}{a} ) \]周囲の長さ
\[ L = 2 \sqrt{h^2 + \frac{a^2}{4} } + a \]面積
\[ S = \frac{1}{2}ah \]EXCELの数式
| A | B | |
|---|---|---|
| 1 | 高さ(h) | 100 |
| 2 | 底辺(b) | 80 |
| 3 | 斜辺の長さ(a) | =SQRT(B1^2 + B2^2/4) |
| 4 | 角度(θ) | =DEGREES(ATAN(2*B1/B2)) |
| 5 | 面積(S) | =B1*B2/2 |
直角二等辺三角形
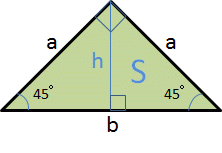
高さ
\[ h = \frac{b}{2} \]斜辺の長さ
\[ a = \frac{b}{\sqrt{2}} \]周囲の長さ
\[ L = (1+\sqrt{2})b \]面積
\[ S = \frac{b^2}{4} \]EXCELの数式
| A | B | |
|---|---|---|
| 1 | 底辺の長さ(b) | 100 |
| 2 | 高さ(h) | =B1/2 |
| 3 | 斜辺の長さ(a) | =B1/SQRT(2) |
| 4 | 周囲の長さ(L) | =(1+SQRT(2))*B1 |
| 5 | 面積(S) | =B1^2/4 |