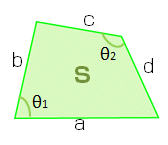
ブレートシュナイダーの公式(円に内接しない場合)
面積
\[ S = \sqrt{ (s-a)(s-b)(s-c)(s-d)-abcd \cdot \cos^{2}( \frac{\theta}{2} ) } \]
\[ \star s = \frac{a+b+c+d}{2} \ \ \ \ \ \star \theta = \theta_1 + \theta_2 \]
辺の長さ
\[ L = 2s = a + b + c + d \]
EXCELの数式
| A | B |
|---|
| 1 | 辺(a) | 30 |
|---|
| 2 | 辺(b) | 40 |
|---|
| 3 | 辺(c) | 20 |
|---|
| 4 | 辺(d) | 30 |
|---|
| 5 | 対角の和(θ1+θ2) | 160 |
|---|
| 6 | 計算過程(s) | =(B1+B2+B3+B4)/2 |
|---|
| 7 | 周囲(L) | =SQRT( (B6-B1)*(B6-B2)*(B6-B3)*(B6-B4)
- B1*B2*B3*B4*COS(RADIANS(B5/2))^2 ) |
|---|
| 8 | 面積(S) | =2*B6 |
|---|
不等辺の四角形(円に内接する場合)
面積
\[ S = \sqrt{ (s-a)(s-b)(s-c)(s-d) } \ \ \ \ \ \ \star s = \frac{ a+b+c+d }{ 2 } \]
周囲の長さ
\[ L = 2s = a+b+c+d \]
EXCELの数式
| A | B |
|---|
| 1 | 辺(a) | 3 |
|---|
| 2 | 辺(b) | 4 |
|---|
| 3 | 辺(c) | 5 |
|---|
| 4 | 辺(d) | 6 |
|---|
| 5 | 計算過程 | =(B1+B2+B3+B4)/2 |
|---|
| 6 | 周囲の長さ(L) | =B1+B2+B3+B4 |
|---|
| 7 | 四角形の面積(S) | =SQRT((B5-B1)*(B5-B2)*(B5-B3)*(B5-B4)) |
|---|