楕円体の公式(体積・表面積)
楕円体
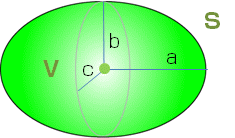
計算
体積
\[ V = \frac{4}{3} \pi abc \]表面積(近似式)
p = 1.6075 のとき最大誤差は1.061% の近似式 \[ S \approx 4 \pi \left( \frac{ a^p b^p + a^p c^p + b^p c^p}{3} \right) ^ { \frac{1}{p} } \]表面積
\[ S = 2 \pi \left( c^2 + b \sqrt{a^2-c^2} E\left(x,k\right) + \frac{bc^2}{ \sqrt{a^2-c^2} } F\left(x,k\right) \right) \] \[ \ \ \ k = \frac{b^2-c^2}{ b^2 \sin^2 x} \] \[ \ \ \ F(x,k) =\int_0^x \frac{1}{ \sqrt{ (1-t^2)(1-k^2 t^2)} } dt \] \[ \ \ \ E(x,k) =\int_0^x \sqrt{ \frac{1 - k^2 t^2}{ 1 - t^2 } } dt \]EXCELの数式
| A | B | |
|---|---|---|
| 1 | 半径(a) | 2 |
| 2 | 半径(b) | 3 |
| 3 | 半径(c) | 5 |
| 4 | 体積(V) | =4/3 * PI()*B1*B2*B3 |
| 5 | 表面積(S *近似式) | =4*PI()*(((B1^1.6075*B2^1.6075+B1^1.6075*B3^1.6075 +B2^1.6075*B3^1.6075)/3)^(1/1.6075)) |