EXCEL 正規分布 NORMDIST関数
正規分布(ガウス分布)の確率密度と累積分布
正規分布のグラフの特徴は、グラフの面積が1になる事です。そこから確率を知る事ができます。
どういう事か？は 平均300、偏差10の正規分布のグラフを例にその意味をEXCELのNORMDIST関数を用いて解説します。
NORMDIST関数
=NORMDIST(x, 平均(μ), 標準偏差(σ), 関数形式)
関数形式・・・Trueの場合は累積分布関数の値、Falseの場合は確立密度関数の値(グラフのY値)この関数形式の違いによる意味も見ていきましょう。
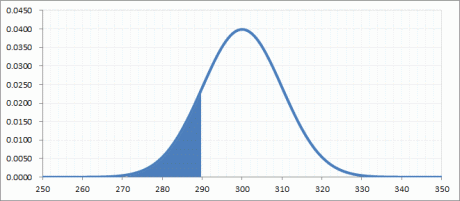
x=290の場合
| 数式 | 結果 | 備考 |
|---|---|---|
| =NORMDIST(290, 300, 10, True) | 0.15865526 | 290以下になる確率は15.8%です。 ＊グラフで青く塗られた部分です。 |
| =NORMDIST(290, 300, 10, False) | 0.024197072 | Yの値。290ピッタリになる確率が2.4% |
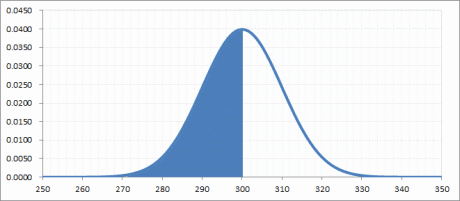
x=300の場合
| 数式 | 結果 | 備考 |
|---|---|---|
| =NORMDIST(300, 300, 10, True) | 0.5 | 300以下になる確率は50%です |
| =NORMDIST(300, 300, 10, False) | 0.039894228 | Yの値。300ピッタリになる確率が3.9% |
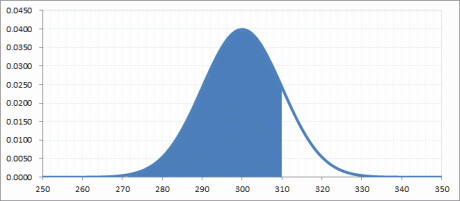
x=310の場合
| 数式 | 結果 | 備考 |
|---|---|---|
| =NORMDIST(310, 300, 10, True) | 0.84134474 | 310以下になる確率は84%です |
| =NORMDIST(310, 300, 10, False) | 0.024197072 | Yの値。310ピッタリになる確率が2.4% |
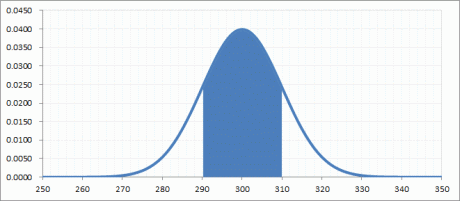
290～310に入る確率を求める
290～310に入る確率は =NORMDIST(310, 300, 10, True)-NORMDIST(290, 300, 10, True) で求める事ができます。
| 数式 | 結果 | 備考 |
|---|---|---|
| =NORMDIST(310, 300, 10, True) | 0.84134474 | 310以下になる確率は84%です |
| =NORMDIST(290, 300, 10, True) | 0.15865526 | 290以下になる確率は15.8%です |
| =0.84134474-0.15865526 | 0.68268948 | 290～310に入る確率は68.2%です |
このように、ちょっとしたデータがあれば簡単に、平均(μ)と偏差(σ)を求め、NORMDIST関数 を使用することにより、様々な場合の確率を導く事ができます。
「正規分布(ガウス分布)とは？」へ戻る