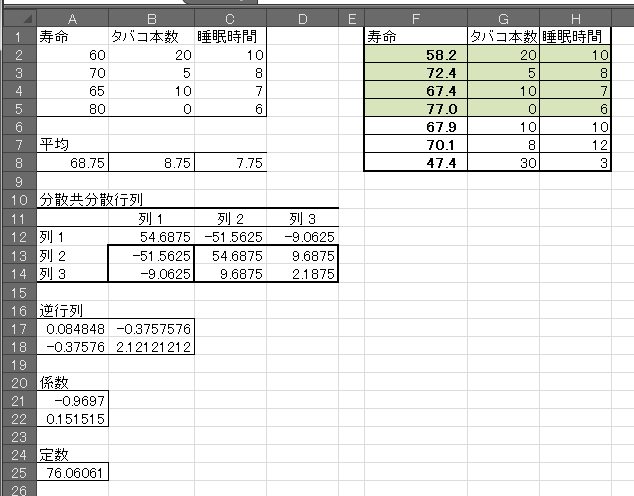
EXCELгҒ§йҮҚеӣһеё°ејҸ(еӨҡеӨүйҮҸи§Јжһҗ)
гҖҖEXCELгҒ§еӨҡеӨүйҮҸи§ЈжһҗгҒ®д»•ж–№гӮ’и§ЈиӘ¬гҒ—гҒҫгҒҷгҖӮеӨҡеӨүйҮҸи§ЈжһҗгҒЁгҒ„гҒҶгҒ®гҒҜдҫӢгҒҲгҒ°гҖҒ гҖҢгӮҝгғҗгӮі1ж—ҘдҪ•жң¬еҗёгҒҶпјҹ1ж—ҘгҒ®зқЎзң жҷӮй–“гҒҜпјҹ1ж—ҘгҒ®ж‘ӮеҸ–гӮ«гғӯгғӘгғјгҒҜпјҹгҖҚ гҒӘгҒ©гҒӢгӮүгҖҒгӮәгғҗгғӘгҖҢгҒӮгҒӘгҒҹгҒ®еҜҝе‘ҪгҒҜxxxжүҚгҒ§гҒҷпјҒгҖҚгҒЁгҒ„гҒҶдәӢгӮ’зөұиЁҲзҡ„гҒӘжүӢжі•гҒӢгӮүзӯ”гҒҲгӮӢж–№жі•гҒ§гҒҷгҖӮ
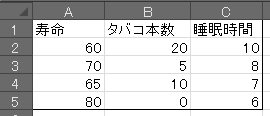 гҒ“гҒ®гӮҲгҒҶгҒӘгғҮгғјгӮҝгҒҢгҒӮгӮҢгҒ°гҖҒ
гҒ“гҒ®гӮҲгҒҶгҒӘгғҮгғјгӮҝгҒҢгҒӮгӮҢгҒ°гҖҒгӮҝгғҗгӮі20жң¬гҖҒзқЎзң 3жҷӮй–“гҒ®е ҙеҗҲгҒҜ57.1жӯігҖӮ
гӮҝгғҗгӮі0жң¬гҖҒзқЎзң 10жҷӮй–“гҒ®е ҙеҗҲгҒҜ77.6жӯігҖӮ
гҒ®гӮҲгҒҶгҒ«гғҮгғјгӮҝгҒ«гҒҜгҒӘгҒ„зӯ”гҒҲгӮ’е°ҺгҒҸдәӢгҒҢгҒ§гҒҚгҒҫгҒҷгҖӮ
EXCELгҒ§йҮҚеӣһеё°ејҸгӮ’жұӮгӮҒгӮӢ
иЁҲз®—гҒ®жөҒгӮҢ
гҖҖиЁҲз®—гҒ®жөҒгӮҢгҒҜгҖҒдёҖз•ӘдёҠгҒ«з”Ёж„ҸгҒ•гӮҢгҒҹгғҮгғјгӮҝгҒӢгӮүй ҶгҒ«иЁҲз®—гҒ—гҒҰгҒ„гҒҚгҖҒжңҖзөӮзҡ„гҒ«гҒҜдёӢгҒ«гҒӮгӮӢгҖҢдҝӮж•°гҖҚгҒЁгҖҢе®ҡж•°гҖҚгӮ’жұӮгӮҒгӮӢдәӢгҒҢгҒ§гҒҚгӮҢгҒ°йҮҚеӣһеё°ејҸгӮ’жұӮгӮҒгӮӢдәӢгҒҢгҒ§гҒҚгҒҫгҒҷгҖӮ гҒ“гҒ®йҮҚеӣһеё°ејҸгҒ«гӮҲгӮҠгҖҒгғҮгғјгӮҝгҒ«гҒҜгҒӘгҒ„жқЎд»¶гҒ®зӯ”гҒҲгҖҢгӮҝгғҗгӮі40жң¬гғ»зқЎзң жҷӮй–“5жҷӮй–“гҒ®е ҙеҗҲгҒ®еҜҝе‘ҪгҒҜпјҹгҖҚгҒӘгҒ©гӮ’иҮӘз”ұгҒ«жұӮгӮҒгӮӢдәӢгҒҢгҒ§гҒҚгҒҫгҒҷгҖӮ гҒҫгҒҹгҖҒгҒ“гҒ®гғҡгғјгӮёгҒ§гҒҜгҖҒж•°еӯҰзҡ„гҒӘж„Ҹе‘ігҒ®и§ЈиӘ¬гҒҜзңҒгҒҚгҖҒж•°еӯҰзҡ„гҒӘж„Ҹе‘ігҒҜеҲҘгғҡгғјгӮёгҒ§и§ЈиӘ¬гҒ—гҒҫгҒҷгҖӮ
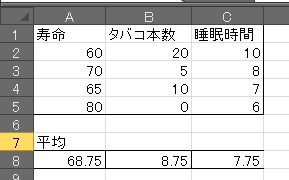
гӮөгғігғ—гғ«гғҮгғјгӮҝгғјгҒ®е№іеқҮеҖӨ
в‘ гҒҫгҒҡз”Ёж„ҸгҒ•гӮҢгҒҹ3еҲ—гҒ®гғҮгғјгӮҝгҒӢгӮүгҒҜгҒқгӮҢгҒһгӮҢгҒ®е№іеқҮеҖӨгҖҢ=AVERAGE(пҪһ)гҖҚгӮ’з®—еҮәгҒ—гҒҫгҒҷгҖӮ
(еҫҢгҒ§дҪҝз”ЁгҒ—гҒҫгҒҷгҖӮ)
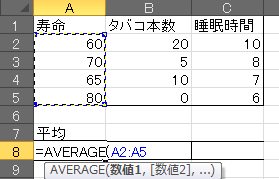
в‘Ўе№іеқҮеҖӨгӮ’жұӮгӮҒгҒҫгҒ—гҒҹ
еҲҶж•Је…ұеҲҶж•ЈиЎҢеҲ—
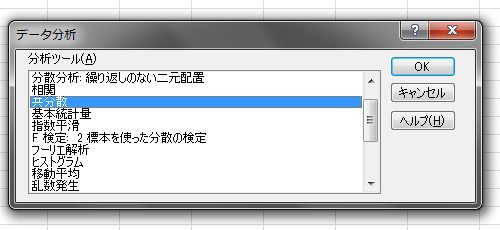
гӮўгғүгӮӨгғігҖҢеҲҶжһҗгғ„гғјгғ«гҖҚгӮ’гӮӨгғігӮ№гғҲгғјгғ«гҒ—гҒҰгҒҠгҒҸеҝ…иҰҒгҒҢгҒӮгӮҠгҒҫгҒҷгҖӮ
в‘ўEXCEL2010гҒ®е ҙеҗҲгҖҢгғҮгғјгӮҝгҖҚгғЎгғӢгғҘгғјвҶ’гҖҢгғҮгғјгӮҝеҲҶжһҗгҖҚвҶ’гҖҢгғҮгғјгӮҝеҲҶжһҗгҖҚгғҖгӮӨгӮўгғӯгӮ°вҶ’гҖҢе…ұеҲҶж•ЈгҖҚгӮ’йҒёжҠһгҒ—гҒҰOKгӮ’гӮҜгғӘгғғгӮҜгҒ—гҒҫгҒҷгҖӮ
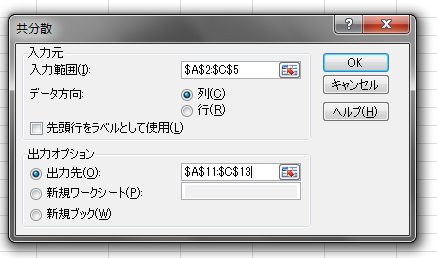
в‘ЈгҖҢе…ҘеҠӣе…ғгҖҚгҒҜз”Ёж„ҸгҒ•гӮҢгҒҹгғҮгғјгӮҝгҖҢA2:C5гҖҚгӮ’йҒёжҠһгҒ—гҖҒгҖҢеҮәеҠӣе…ҲгҖҚгҒҜйҒ©еҪ“гҒӘе ҙжүҖгӮ’йҒёжҠһ(гҒ“гҒ“гҒ§гҒҜA11:C13)гҒ—гҒҫгҒҷгҖӮ
гӮўгғүгӮӨгғігҖҢеҲҶжһҗгғ„гғјгғ«гҖҚгӮ’гӮӨгғігӮ№гғҲгғјгғ«гҒ—гҒҰгҒҠгҒҸеҝ…иҰҒгҒҢгҒӮгӮҠгҒҫгҒҷгҖӮ
в‘ӨгҖҢеҲҶж•Је…ұеҲҶж•ЈиЎҢеҲ—гҖҚгҒҢжұӮгҒҫгӮҠгҒҫгҒ—гҒҹ
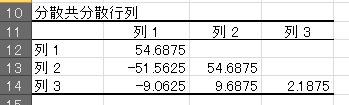
гҒҫгҒҹгҖҒеҫҢгҒ§иЁҲз®—гҒ§дҪҝз”ЁгҒҷгӮӢгҒҹгӮҒгҖҒз©әзҷҪйғЁеҲҶгӮ’д»ҘдёӢгҒ®гӮҲгҒҶгҒ«еҹӢгӮҒгҒҰгҒҠгҒҚгҒҫгҒҷгҖӮ
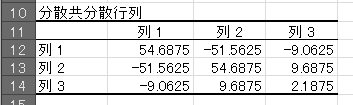
йҖҶиЎҢеҲ—
в‘Ҙе…ҲзЁӢжұӮгӮҒгҒҹеҲҶж•Је…ұеҲҶж•ЈиЎҢеҲ—гҒ®еҸідёӢ2иЎҢ2еҲ—гҒ®йҖҶиЎҢеҲ—гӮ’жұӮгӮҒгҒҫгҒҷгҖӮ
A17:B18гӮ’йҒёжҠһгҒ—гҒҹзҠ¶ж…ӢгҒ§вҮ’гҖҢ=MINVERSE(C13:D14) гҖҚвҮ’гҖҢCtrl+Shift+EnterгҖҚ
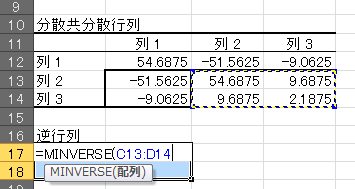
в‘ҰйҖҶиЎҢеҲ—гӮ’жұӮгӮҒгҒҫгҒ—гҒҹ
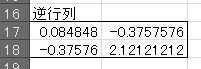
йҮҚеӣһеё°ејҸгҒ®дҝӮж•°гҒ®з®—еҮә
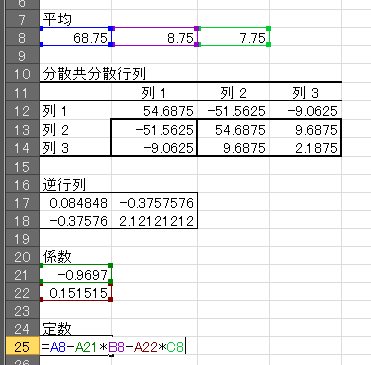
⑧A21:A22гӮ’йҒёжҠһгҒ—гҒҹзҠ¶ж…ӢгҒ§вҮ’гҖҢ=MMULT(A17:B18, B13:B14) гҖҚвҮ’гҖҢCtrl+Shift+EnterгҖҚ
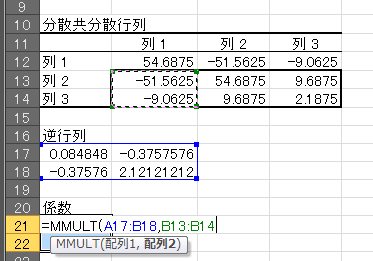
йҮҚеӣһеё°ејҸгҒ®е®ҡж•°гҒ®з®—еҮә
в‘Ёе®ҡж•°гӮ’з®—еҮәгҒ—гҒҫгҒҷгҖӮ⑧гҒ§жұӮгӮҒгҒҹдҝӮж•°гҒЁгҖҒв‘ЎгҒ§жұӮгӮҒгҒҹе№іеқҮеҖӨгҒӢгӮүжұӮгӮҒгҒҫгҒҷгҖӮгҖҢ=A8-A21*B8-A22*C8гҖҚ
йҮҚеӣһеё°ејҸгҒ®дҝӮж•°гҒЁе®ҡж•°гҒӢгӮүзөҗжһңгӮ’жұӮгӮҒгӮӢгҖӮ
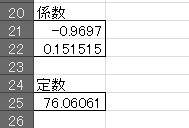
дҝӮж•°гҒЁе®ҡж•°гӮ’жұӮгӮҒгӮӢдәӢгҒҢгҒ§гҒҚгҒҫгҒ—гҒҹгҖӮA21гҒҜгҖҢгӮҝгғҗгӮігҒ®жң¬ж•°гҖҚгҒ®дҝӮж•°гҖҒA22гҒҜгҖҢзқЎзң жҷӮй–“гҖҚгҒ®дҝӮж•°гҒ«гҒӘгӮҠгҖҒд»ҘдёӢгҒ®ејҸгҒ§жұӮгӮҒгӮӢдәӢгҒҢгҒ§гҒҚгҒҫгҒҷгҖӮ
еҜҝе‘Ҫ = A21*гӮҝгғҗгӮігҒ®жң¬ж•° + A22*зқЎзң жҷӮй–“ + A25
гҒ“гҒ®дҝӮж•°гғ»е®ҡж•°гӮ’з”ЁгҒ„гҒҰF2:H5гҒ«гҒҜе…ғгғҮгғјгӮҝгҒ®гғ‘гғ©гғЎгғјгӮҝгӮ’гҒӮгҒҰгҒҜгӮҒгҒҹзөҗжһңгҖҒF6:H8гҒҜе…ғгғҮгғјгӮҝгҒ«гҒҜгҒӘгҒ„гғ‘гғ©гғЎгғјгӮҝгӮ’еҪ“гҒҰгҒҜгӮҒгҒҹзөҗжһңгҒ§гҒҷ