正規分布(ガウス分布)とは？

　正規分布は是非理解しておきたい手法です。正規分布を鉛筆を使って計算するとすごく大変なのですが、EXCELを用いれば NORMDIST関数を使用するだけで完結します。もし正規分布は何ぞや？という方は是非このページなどで概念を理解してみて下さい。既に詳しい方はこちらでNORMDIST関数の使用例を解説しています。

正規分布(ガウス分布)とは？

　例えばコンビニで500mlのお茶を100本買ってきて、100本すべて何ml入っているか？を確認したとしましょう。おそらく、平均をすればほぼ500mlですが、±1ml(499 or 501ml)が30本、±2ml(498ml or 502ml)が20本・・・のように分布すると思います。もしかしたら1万本に1本は480ml　とすごく量が少ないお茶があるかもしれません。これをグラフに描くと以下のようになるのは直観的に理解できると思います。

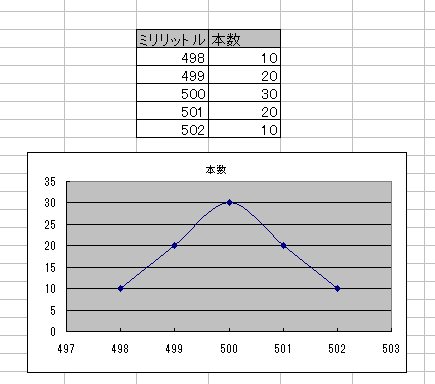
　このグラフのポイントは 平均値が一番多く、平均値からずれるにしたがって少なくなっていく「山の形」のグラフです。「コンビニのお茶」以外にも、世の中の多くの事象が、このような山の形となります。このような山の形の分布を「正規分布」といいます。サンプル数が多ければ多いほど山が美しい形になっていきます。

「偏差」機械でいれた場合と手でいれた場合？

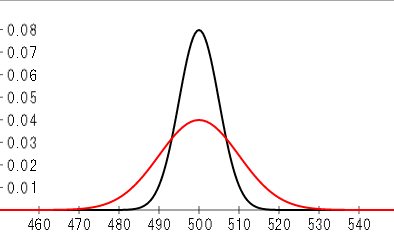
ペットボトルにお茶を入れる作業は機械で行われていると思いますが、人の手でで行った場合はどうなるか？きっと、機械より容量のバラつきが大きくなります。このバラつきを「偏差」と言います。イメージとして、以下の図の黒いグラフは機械でいれた場合、赤いグラフは手でいれた場合です。機械のほうが平均である500mlに集中しばらつきが少ないですが、人手のほうでは平均500mlであっても少なくバラつきが多いというのを表しています。

正規分布のグラフ

方法	平均(μ)	偏差(σ)
機械で	500ml	5ml
人手で	500ml	10ml

このグラフは平均(μ：ミュー)と偏差(σ：シグマ)の2つの数値だけで作る事ができます。エクセルで平均は AVERAGE関数、偏差は STDEV関数を用いれば算出できます。

正規分布の公式

　正規分布は以下の公式から求める事ができます。でも、ちょっと覚えるのがやっかいですので、無理に暗記する必要はありません。平均と偏差の2つだけわかれば、この公式から上図のようなグラフを作成できるとだけ覚えておいて下さい。

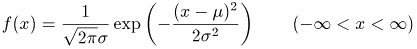
今回のような機械か人手か？の場合では σに5を入れた場合は黒いグラフ、σに10を入れた場合は赤いグラフになります。 μ(平均)には500を設定し、xにはとりあえず 460ml～540mlまでの値でもどんどん入れてグラフにプロットすると上図のようになります。

正規分布の数式とグラフで平均と偏差の挙動を見る

以下表の平均と偏差の数値で3種類のグラフを作成しました。正規分布の数式とグラフから覚えておきたいポイントは4つです。

①グラフのピークとなっているところが平均値。
②平均(μ)が変わると山が左右に動く(例：赤と青のグラフ)。
③偏差(σ)が小さければ山が尖り、大きければ山がなだらかになる(例：赤と黒のグラフ)。
④山の面積はいずれも1。

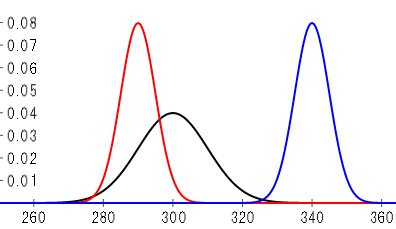
グラフ	平均(μ)	偏差(σ)
黒	300	10
赤	290	5
青	340	5

上記のようなグラフを正規分布のグラフをEXCELで作成する

「正規分布の確率密度と累積分布」でより正規分布の本当の使い方を解説。